encodeNumber(6936)

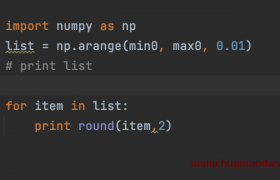
美国程序员面试题：

The fundamental theorem of arithmetic states that every natural number greater than 1 can be written as a unique product of prime numbers. So, for instance, 6936=2*2*2*3*17*17. Write a method named encodeNumber what will encode a number n as an array that contains the prime numbers that, when multipled together, will equal n. So encodeNumber(6936) would return the array {2, 2, 2, 3, 17, 17}. If the number is <= 1 the function should return null;
-5
if n is
return
because
10
5
because the prime factors of 10 are 2 and 5 and 5 is the largest one.
6936
17
because the distinct prime factors of 6936 are 2, 3 and 17 and 17 is the largest
1
0
because n must be greater than 1
If you are programming in Java or C#, the function signature is
int[ ] encodeNumber(int n)
If you are programming in C or C++, the function signature is
int *encodeNumber(int n) and the last element of the returned array is 0.
Note that if you are programming in Java or C#, the returned array should be big enough to contain the prime factors and no bigger. If you are programming in C or C++ you will need one additional element to contain the terminating zero.
Hint: proceed as follows:
1. Compute the total number of prime factors including duplicates.
2. Allocate an array to hold the prime factors. Do not hard-code the size of the returned array!!
3. Populate the allocated array with the prime factors. The elements of the array when multiplied together should equal the number.

测试样例：

java实现代码

package com.zzy;

import java.util.ArrayList;

/**
 * 更多请关注: http://huamaodashu.com
 * Created by hadoopall on 27/07/2018.
 */
public class encodeNumber {
    public static void main(String[] args) {

        int n =-18;
        System.out.println(encodeNumber(n));

    }

    public static int[] encodeNumber(int n){
        ArrayList arrayList = new ArrayList();
        if(n <= 1){
            return null;
        }else {
            int i = 2;


            while (n>1){

                if(isPrimeNumber(i)){
                    if(n%i==0){

                        arrayList.add(i);
                        n=n/i;
                    }else {
                        i++;
                    }


                }else {
                    i++;
                }

            }
        }
        int [] encodearray = new int[arrayList.size()];
        for (int i = 0; i < arrayList.size(); i++) {
            encodearray[i] = (int)arrayList.get(i);
            System.out.println(encodearray[i]);
        }
        return encodearray;

    }


    //判断一个数是否为素数
    public static boolean isPrimeNumber(int num){

        if(num == 2){
            return true;// 对2单独处理
        }
        if(num < 2 || num % 2 == 0){
            return false; // 识别小于2的数和偶数
        }
        for (int i =3; i<=Math.sqrt(num);i+=2){
            if(num % i == 0){  // 识别被奇数整除
                return false;
            }
        }
        return true;
    }

}